How to Find Tangent Line of an Ellipse

In Sympy the function tangent_lines returns Tangent lines between p point and the ellipse. Make a copy of the 2 ellipses a known distance from the originals.

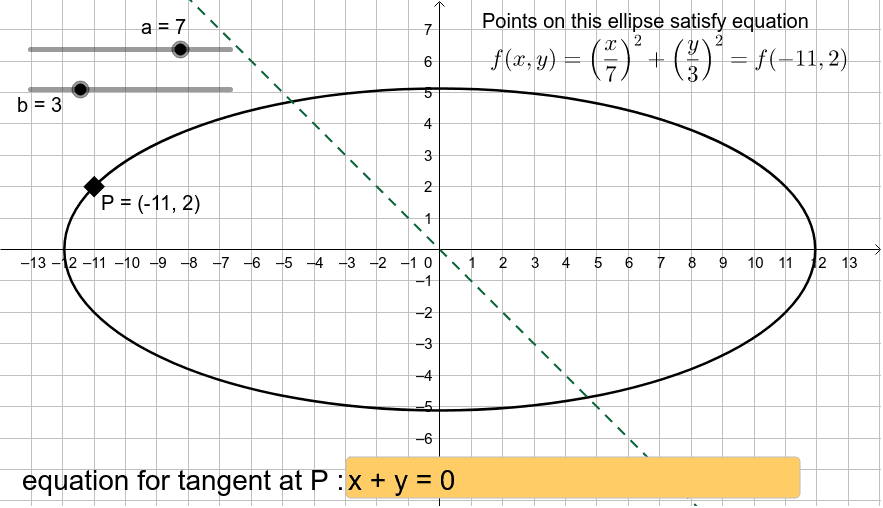
Find Tangent To Ellipse Geogebra

If the line y mx c touches the ellipse x 2 a 2 y 2 b 2 1 then c 2 a 2 m 2 b 2.

. The straight line y mx a 2 m 2 b 2 represent the tangents to the ellipse. For tangents lines connecting 2 ellipses. Find the tangent line equation and the guiding vector of the tangent line to the ellipse at the point.

The equation of the tangent line to ellipse at the point x_0y_0 is y-y_0mx-x_0 where m is the slope of the tangent. If you want the unit tangent and normal vectors you need to divide the two above vectors by their length which is equal to. The ellipse is parametrized so Im not sure how to write the code to find the tangent line.

A straight line in the plane is said to be tangent to an ellipse if the intersection between these two is given by a single point called the point of tangency. No matter how you reshape the ellipse the tangent line makes equal angles to each generator line ab. 1 Find the first derivative of fx.

Y Use the parametric equations of an ellipse x 2 cos e y11 sine 0. What do you recommend I add to find the tangent line at the point x ay a. In this tutorial students will learn how to find the equation of tangents to an ellipse at a specific point.

X 2 a 2 y 2 b 2 1 i Now differentiating equation i on both sides with respect to x we have. I have discussed two methods. Function destin_ellipse xRadiusyRadius csqrt xRadius2-yRadius2.

Again press Ctrl Right Click of the mouse and choose Tangent. We have the standard equation of an ellipse. The students will use implicit differentiation.

2 Plug x value of the indicated point into f x to find the slope at x. Draw in your two Circles if you dont have them already drawn. There are two tangents parallel to any given direction.

I have to find the tangent line of an ellipse that I have written code for. In the figure above click show perpendicular. Pick the first circles outline.

Write the answer in the form ymxb. The perpendicular from the tangent through the contact point bisects the angle between generator lines. Answer 1 of 4.

Consider that the standard equation of ellipse with vertex at origin 0 0 can be written as. The ellipse is parametrized so Im not sure how to write the code to find the tangent line. This is waht I have so far.

Find the equation of the tangent line to the curve 3t2 1 23 125 y that passes through the point 76 375. 2 x a 2 2 y b 2 d y d x 0 y b 2 d y d x x a 2 d y d x b 2 x a 2 y. Move the contact point or.

Using implicit differentiation to find the equation of the tangent line is only slightly different than finding the equation of the tangent line using regular differentiation. The equations of tangent and normal to the ellipse x 2 a 2 y 2 b 2 1 at the point x 1 y 1 are x 1 x a 2 y 1 y b 2 1 and a 2 y 1 x b 2 x 1 y a 2 b 2 x 1 y 1 0 respectively. List with 1 or 2.

Find the equation of the tangent and normal to the ellipse x 2 a 2 y 2 b 2 1 at the point a cos. If p is on the ellipse returns the tangent line through point p. The different forms of the tangent equation are given below.

Please respond as soon as possible. 3 Plug x value into fx to find the y coordinate of the tangent point. Implicit differentiation is just the regular way of doing things but we throw in the chain rule t.

Slope form of a tangent to an ellipse. 4 Combine the slope from step 2 and point from step 3 using the point-slope. Take the derivative of the given function.

The equation for the tangent line can be found using the formula for a line when the slope and one point are known. What do you recommend I add to find the tangent line at the point xaya. The Equation of tangent to the given ellipse whose slope is m is.

When is a straight line and tangent to the ellipse. The perpendicular line you now see bisects the angle between the two generator lines a and b. Extend the lines on.

Y - n slope x - m -mn b2a2 x - m After a lot of algebra this can be reorganized into the form. Hey GuysIn this tutorial i will demonstrate as to how tangent and normal can be made at any point on the ellipse. Y mx a 2 m 2 b 2 Point of contact are a 2 m a 2 m 2 b 2 b 2 a 2 m 2 b 2.

Please respond as soon as possible. This is waht I have so far. Otherwise returns the tangent line s from p to the ellipse or None if no tangent line is possible eg p inside ellipse.

Start Line command and then press Ctrl Right Click of the mouse and choose Tangent. Note that there are two tangents to the ellipse having the same m ie. Displaystyle fracx2a2fracy2b21tag1 Find an equation of a tangent line at a point x_0y_0 at this ellipse 1 is begging for implicit differentiation.

Zoom in to the originals and you will see the lines intersect the larger ellipses at 2 places each forming an arc. So the unit tangent vector and the unit normal vector are and respectively. Remember that we follow these steps to find the equation of the tangent line using normal differentiation.

Draw lines connecting the quadrants of the 2 ellipses. A line which intersects the ellipse at a point is called a tangent to the ellipse. A2n ya2n2 b2m2 b2 m x a2n2 b2m2 1.

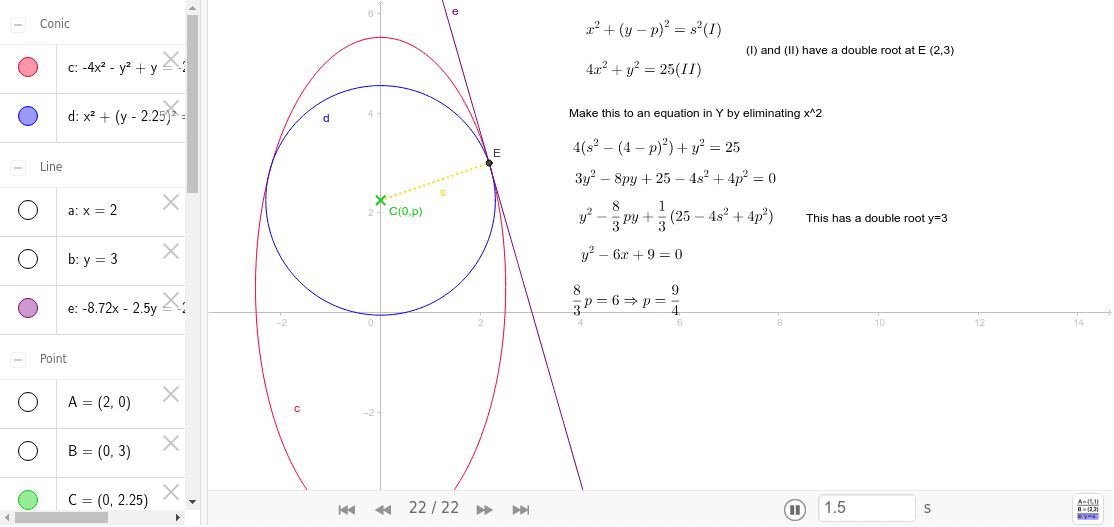
Descartes Method For Finding The Tangent Line To An Ellipse Geogebra

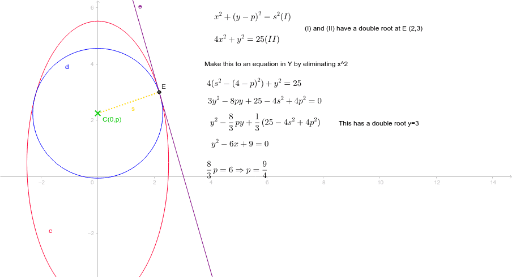
Descartes Method For Finding The Tangent Line To An Ellipse Geogebra

Slope Of The Tangent Line For An Ellipse Youtube